マルチファクターモデルを考えていく上では、資産価格の変動要因であるファクターが重要な役割になってきます。どのようなファクターを選択するかという方法については、
ファーマフレンチのファクターモデルのように意味的に定義するものや
主成分分析や因子分析で共通要因を機械的に見つける方法
を見てきました。
ここでは、ファクターのリターンと、ファクターエクスポージャーの関係性について整理していきます。
ファクターリターン、ファクターエクスポージャーと個別リターン
個別資産のリターンを考える場合には、基本的にファクターリターンとファクターエクスポージャーを掛け合わせた数値をすべて足し合わせることで、個別資産のリターンとすることができます。
例えば、株式Aは小型バリュー株、株式Bは大型グロース株、株式Cは小型グロース株だったとします。
以下の表に、マーケットファクター、サイズファクター、バリューファクターの各ファクターリターンと、株式A、B、Cの各ファクターエクスポージャーを整理します。
| ファクター/株式 | マーケットファクター | サイズファクター | バリューファクター |
|---|---|---|---|
| ファクターリターン(%) | 1.5 | -0.5 | 2.0 |
| 株式A | 1.2 | 0.8 | 1.5 |
| 株式B | 1.0 | -1.2 | -0.5 |
| 株式C | 1.3 | 0.5 | -1.0 |
株式AとCはサイズファクターがプラスとなっていますがこれは、小型株ということを示しています。(ファクターリターンは小型株のリターンが高いとなるので、エクスポージャーは小型株の場合はプラスになります。)
また、株式Aはバリューなので、バリューファクターがプラス、株式BとCはグロースなので、バリューファクターはマイナスになります。
ここで、各株式のリターンは次の式で求められます:
株式Aのリターン
株式Bのリターン
株式Cのリターン
このように、ファクターモデルを用いることで各株式のリターンを求めることができます。ファクターリターンとファクターエクスポージャーの組み合わせによって、個別の資産リターンが異なることがわかります。この方法を用いることで、資産価格の変動要因を分析し、ポートフォリオのパフォーマンスをより精緻に理解することが可能になります。
ファクターエクスポージャーの定義方法
前項では、ファクターリターンと、ファクターエクスポージャーがわかれば、ファクターモデルに基づいて、個別銘柄のリターンの推定が可能になることを確認しました。
ファクターリターンについては、ファーマフレンチのファクターモデルで説明したような方法や、主成分分析、因子分析を用いたファクター生成で紹介した方法が使えます。
しかし、各銘柄のファクターエクスポージャーの部分はどのように決めればよいのでしょうか?
個別銘柄の特性値を使う
最も単純な方法は、ファクターの意味に基づいて、個別銘柄の特性値を使うことです。
具体的には、サイズファクターのエクスポージャーであれば、時価総額を用いることができます。(実際には時価総額の対数値を用いることが多いです)サイズファクターは小型株の大きくないといけないので、小型株を基準に考える場合には、逆数にしたりマイナスをつけたりといったことは必要になりますが、時価総額という特徴量を使えば、各銘柄のサイズエクスポージャーを比較できそうです。
バリューファクターの場合には、Book-to-MarketやPER、配当利回りなどが使えるかもしれません。
このように、個別の銘柄の財務情報などを用いて、各銘柄の特性値を作成し、それをファクターエクスポージャーとすることができます。
この場合の注意点としては、特性値の分布がどうなるかもある程度確認が必要ということです。特定の値に偏る場合には何らかの工夫が必要になる場合があります。
その他、ファクター同士のエクスポージャーを比較しやすくするために、平均0、標準偏差1になるように正規化することも多いです。正規化をしていない場合は、どのくらい大型なのか、小型なのか数値を言われただけだと、一般的な時価総額の大きさがわかっていないとわかりにくいですが、正規化していれば、値の正負で判断できます。
ファクターリターンと銘柄リターンで回帰する
先ほどの方法は、財務諸表などの情報から個別銘柄の特徴量を作成するので、直感的にもわかりやすかったと思います。しかし、実際には、データの入手が困難で、必要な特性に関する値を得られないことがあります。(そのデータを得るにはデータを購入する必要があるなど)次は、そのような場合に、銘柄のファクターエクスポージャーを推定する方法を紹介していきます。
この方法を使えば、財務諸表の値がわからなくても、各銘柄のリターンと、ファーマフレンチのファクターリターンデータなどから銘柄のファクターエクスポージャーを推定することができます。
その方法は、銘柄リターンをファクターリターンで回帰して、その係数をファクターエクスポージャーにするというものです。
銘柄リターンをこのような重回帰モデルで、rとFがわかっているときに係数$\beta$を求める問題だと考えることで、銘柄リターンrとファクターリターンFの時系列データがあれば、回帰によって、ファクターエクスポージャーを推定できます。
ただし、ここで注意しておかないといけないのは、この場合、$\beta$はこの期間変化しないと考えているということです。ファクターエクスポージャーが時間とともに変化すると考える場合には使えません。多くの場合、$\beta$は多少なりとも変化はしていますが、銘柄のリターンなどに比べるとその変化は非常にゆるかやです。実際に財務諸表の数値を用いるような場合でも更新できるのはせいぜい3か月に1回程度です。したがって、財務的な数値で急激に変化しないと考えられるファクターに対するエクスポージャーはこの方法で求めることができます。
Pythonでファクターエクスポージャーを求めてみる
それでは、実際にPythonで、銘柄リターンとファーマフレンチのファクターリターンを使った重回帰分析によって、ファクターエクスポージャーを求めてみましょう。
データとして、銘柄リターンには、
– 大型バリュー7203(トヨタ)
– 大型グロースとして6920(レーザーテック)
– 小型バリュー8416(高知銀行)
の4銘柄の3ヶ月の日次リターンから求めてみたいと思います。
全体のコードについては、記事の最後にGoogleColabへのリンクを記載しています。
まずは、必要なデータを準備します。
import numpy as np
import pandas as pd
import yfinance as yf
import pandas_datareader.data as web
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# ファーマフレンチのファクターリターンを取得
start_date = '2024-03-01'
end_date = '2024-06-01'
ff_data = web.DataReader('Japan_3_Factors_daily', 'famafrench', start_date, end_date)[0]
ff_data.index = pd.to_datetime(ff_data.index.astype(str),format='%Y-%m-%d')
# 銘柄リターンの取得
tickers = ['7203.T', '6920.T', '8416.T']
stocks = yf.download(tickers, start=start_date, end=end_date)['Adj Close']
returns = stocks.pct_change().dropna()
# 銘柄リターンのデータフレームを準備
returns = returns.rename(columns={
'7203.T': 'トヨタ',
'6920.T': 'レーザーテック',
'8416.T': '高知銀行',
})
続いて、データを結合して日付を合わせ、銘柄ごとに重回帰分析を行い、その係数を記録していきます。
data = pd.merge(returns*100, ff_data, right_index=True,left_index=True)
# 銘柄ごとにファクターエクスポージャーを計算
results = {}
for ticker in returns.columns:
X = data[['Mkt-RF', 'SMB', 'HML']]
y = data[[ticker]]
model = LinearRegression()
model.fit(X, y)
results[ticker] = model.coef_[0]
# 結果のデータフレーム化
results_df = pd.DataFrame(results, index=['Mkt-RF', 'SMB', 'HML']).T
results_df.index.name = 'Ticker'
results_df
結果の表は以下のようになりました。
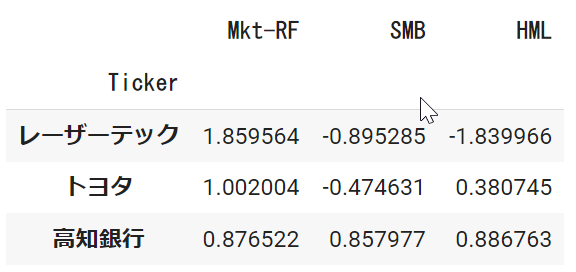
大きさの程度はありますが、レーザーテックと、トヨタはいずれもSMBの係数がマイナスになっており、大型銘柄、高知銀行は小型であることが確認できます。
一方で、HMLに注目するとレーザーテックはマイナスでグロースであるのに対して、トヨタと高知銀行はバリューになっています。実際、自動車メーカーや銀行はバリュー企業が多く回帰の結果も比較的納得ができます。
すべての銘柄に対して、必ずしも推定がうまくいくわけではありませんが、個別のニュースや決算がない期間など銘柄に共通するファクターで動きやすい時には特にうまく推定ができます。
ファクターリターンとファクターエクスポージャーの回帰
鋭い人はもしかすると、ファクターリターンと銘柄のリターンの回帰を見て、ファクターエクスポージャーと個別銘柄リターンから、ファクターリターンを求められるのではないかと思うかもしれません。
まさに、その通りで、時系列方向に対してではなく、クロスセクション方向(たくさんの銘柄を集めた回帰)の回帰を行う場合、同じような方法でファクターリターンを求めることができます。
実際にPythonで具体例を確認してみましょう。
今回はサンプルデータとして、100銘柄のリターン系列、その100銘柄に対する5つのファクターエクスポージャーをランダムに生成します。
ファクターリターンとファクターエクスポージャーの回帰
鋭い人はもしかすると、ファクターリターンと銘柄のリターンの回帰を見て、ファクターエクスポージャーと個別銘柄リターンから、ファクターリターンを求められるのではないかと思うかもしれません。まさに、その通りで、時系列方向に対してではなく、クロスセクション方向(たくさんの銘柄を集めた回帰)の回帰を行う場合、同じような方法でファクターリターンを求めることができます。
実際にPythonで具体例を確認してみましょう。今回はサンプルデータとして、100銘柄のある1か月のリターン系列、その100銘柄に対する5つのファクターエクスポージャーをランダムに生成します。
まず、ランダムなファクターエクスポージャーとリターンデータを生成します。
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# サンプルデータの生成
np.random.seed(42) # 再現性のためのシード
n_stocks = 100 # 銘柄数
n_days = 20 # 日数
n_factors = 5 # ファクター数
# ランダムにファクターエクスポージャーを生成
factor_exposures = np.random.randn(n_stocks, n_factors)
# ランダムにファクターリターンを生成
factor_returns = np.random.randn(n_days, n_factors)
# 銘柄リターンを生成
stock_returns = factor_exposures @ factor_returns.T + np.random.randn(n_stocks, n_days) * 0.1
# データフレームに変換
factor_exposures_df = pd.DataFrame(factor_exposures, columns=[f'Factor_{i+1}' for i in range(n_factors)])
stock_returns_df = pd.DataFrame(stock_returns.T, columns=[f'Stock_{i+1}' for i in range(n_stocks)])
ファクターエクスポージャーと銘柄リターンからファクターリターンを推定します。
# ファクターエクスポージャーを特徴量、銘柄リターンを目的変数として回帰分析を行う
X = factor_exposures_df
factor_return_estimates = []
for day in range(n_days):
y = stock_returns_df.iloc[day]
model = LinearRegression()
model.fit(X, y)
factor_return_estimates.append(model.coef_)
# 結果をデータフレームに変換
factor_return_estimates_df = pd.DataFrame(factor_return_estimates, columns=[f'Factor_{i+1}' for i in range(n_factors)])
先ほどとの違いは、時系列方向ではなく、クロスセクション方向の回帰分析を使ってファクターリターンを推定する方法を確認することができます。
コード全体はこちら



