投資に関する本を読むと、分散投資が大切という内容が書いてあることは多いのではないでしょうか。
しかし、その理由をしっかりと説明しているケースは少ないのではないかと思います。
卵をかごに入れる例を用いて、直感的に説明している場合や、実際のデータを使って、分散投資した場合の結果を理由にしている場合はよくありますが、数学的に説明していることは少ないのではないでしょうか。
今回は、直感的な説明と、数学的な説明の両方から分散投資が重要な理由を考えていきます。
卵を同じかごに入れておくと…
この例はよく説明されるので、既にご存じの方も多いかもしれませんが、
投資においては、卵を一つのかごに入れるなということがよく言われます。
これは、卵を一つのかごに入れておくと、そのかごが落ちたときに、すべての卵が割れてしまうが、複数のかごに分けていた場合は、落ちなかったかごの卵は助かるというものです。
これを投資に置き換える場合は、卵は投資するための資金、かごは投資対象の資産(株など)と考えてもらうとよいかと思います。
具体的に見ていきます。
例えば、100万円の資金を投資することを考えます。
このときに、すべての金額を一つのA社株に投資するというのが、一つのかごにいれるというものです。
一方で、A社株と、B社株と、C社株と、D社株に各25万円ずつ投資するというのが、複数のかごにいれるということです。
例えば、不祥事の発覚によって、A社株の株価が、半分になったとします。これはA社株単体に影響することであるので、他の銘柄の株価は変わらなかったとします。
もし、すべてA社株に投資していれば、資金は半分の50万円になってしまいます。
一方で、4つの銘柄に投資していた場合は、他の銘柄の株価が変わらないので、損失は12.5万円に抑えることができます。
これを銘柄単位ではなく、さらに広げて資産単位で考えることも可能です。
株式だけに投資するよりも、債券や、REIT、コモディティーなど複数の資産に投資した方が、大きな損失が発生する可能性が低くなり、安定した成果を得られるということになります。
ただし、ここで注意しておくべきことは、一つのかごが大きく損失を被った時の影響は複数のかごを使うことによって、減らすことができてよいわけですが、
逆に、大きな利益を出した時にも、その影響は薄まってしまうということです。
つまり、損失が発生する可能性も、利益が発生する可能背もどちらもあり、予測できないからこそ、複数のかごを持つべきなのです。
初めからどれが一番大きな利益を得られるかわかっているのであれば、それにすべての資金を入れた方が効率はいいのです。
分散効果を生かすために重要なこと
また、分散が有効に働くには、もう一つ条件があります。
それは、それぞれの投資対象(かご)が利益を得るか損失を得るかが連動しすぎていると分散効果は薄れるということです。
例えば、分散投資と思って、自動車メーカーA社と自動車メーカーB社の株を持っている場合①と自動車メーカーA社と、飲料メーカーC社の株を持っている場合②の2つを考えてみます。
このとき、自動車を作るための原料が不足し、生産が減少、売り上げも減少しそうだということが起きたとします。
①の場合、どちらも自動車メーカーですから、株価は下がってしまいました。一方で、②の場合は、飲料メーカーの株価は変わらないので、損失は少なくて済みました。
このように、たとえ別々のものに投資しているつもりでも、それらが同じ要因によって変化してしまうのであれば、分散の効果は薄れてしまうのです。
これを数学的に考えると、分散効果を生かすためには、相関の小さい複数の資産に分散して投資をする必要があるということになります。
なぜ分散投資はリスクが低くなるのか
ここまでは、直感的に分散投資が有効である理由を見てきました。
ここからは、数学的に分散投資が有効である理由を考えてみます。
数学と聞くと難しいイメージを持ってしまうかもしれませんが、ここでの計算は中学生や高校生でも追える程度の数式です。
簡素化するために行列などを使おうとすると難しく見えてきますが、基本的な式展開は非常にシンプルです。
簡単のために、ここではA,Bという2つの資産に投資することを考えます。
それぞれの資産に投資した場合のリターンとリスクは以下で与えられたとしましょう。
A:リターン3%、リスク2%
B:リターン6%、リスク8%
また各資産間の相関はAとBの相関0.1とします。
1資産に投資した場合
まずは、一つの資産だけに投資した場合を考えてみましょう。
この場合、作ることのできるポートフォリオは以下の3種類で、それぞれのポートフォリオのリターンとリスクは、
1. A 100%:リターン3%、リスク2%
2. B 100%:リターン6%、リスク8%
となるのは当たり前ですね。
2資産に投資した場合
では、AとBの2資産に投資した場合のリターンとリスクはどうなるでしょうか?
今回は、AとBにそれぞれ50%ずつ投資をしたとして、考えてみます。
この時のリターンは、3%×50%+6%×50%=4.5%
リスクは、
となります。
単純な2資産のリスクの平均の場合は、2%×50%×8%×50%=5%
となり、単純な平均よりも小さくなっていることが確認できます。
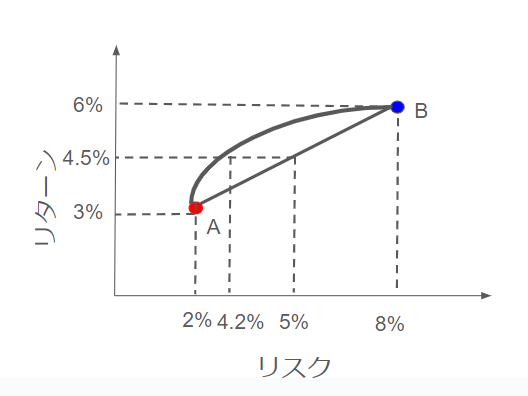
同じリターンが得られるのであれば、当然、リスクは小さい方がよいです。
これをもう少し数学的に示すと、
Aのウェイトを$w_{a}$,リスクを$\sigma_{a}$
Bのウェイトを$w_{b}$,リスクを$\sigma_{b}$
AとBの相関は$\rho$
とすると、リスクは、
これを変形すると
になります。
は正の値のため
つまり、
の分だけ資産AとBを組み合わせたポートフォリオの分散は小さくなります。
ここで、$\rho$は-1から1の間を取るので、-1の時、$\sigma_{ab}$は最小に、1の時に最大になります。
$\rho=1$の時、
になります。
したがって、なるべく相関の小さい資産を組み合わせてポートフォリオを作ることで、リスクを小さくすることができるのです。
多資産への拡張
2資産の場合の数式を多資産の場合に拡張すると、やや複雑になりますが、次のように表現できます。
まず、リターンは、各資産の期待リターンを$\mu_{i}$とすると
リスクは、
と表すことができる。
この多資産のリスクを小さくするためには、なるべく各資産間の相関が小さくなる必要があることがわかります。



