平均分散アプローチとその問題点
以前の記事では、平均分散アプローチに基づいて、最適な資産配分を決める方法をご紹介しました。平均分散アプローチは、比較的簡単な方法で、最適なポートフォリオ比率を決定できる方法であり、ポートフォリオ構築においてよく用いられる手法ですが、欠点もあります。それは、平均分散アプローチによって、最適な比率を知るためには、入力として、各資産の期待リターンと、リスクが必要ということです。
特に期待リターンは、推定が難しく、推定誤差が大きいことが知られています。直感的には、過去のnか月のリターンの平均などを取ればいいように思いますが、、実際は、過去nか月リターンとその後mか月のリターンが大きく異なっているということがよく起こります。平均分散アプローチはリターンとリスクが正しく推定できていることを前提に最適な比率を決めますので、間違ったリターンを入力していると全く効率的ではないポートフォリオを持つことになってしまうのです。
そこでよく用いられるのがブラックリッターマンモデルに基づくポートフォリオ構築です。このブラックリッターマンモデルは、平均分散アプローチの欠点である期待リターンの推定という問題を解決しつつ、投資家が考える見通しも理論的な枠組みと組み合わせることができる方法です。
ブラックリッターマンモデルの流れ
ブラックリッターマンモデルは次のような流れで最適なポートフォリオ配分を決定していきます。
1. 市場が効率的であると仮定して逆算的に各証券の均衡期待リターンを求める
2. 投資家の見通しを均衡期待リターンと組み合わせてリターンとリスクを更新する
3. 更新されたリターンとリスクをもとに平均分散アプローチと同様に最適化を行いポートフォリオのウェイトを決定する。
均衡期待リターンを求める
ブラックリッターマンモデルにおける最初の一歩は、各資産あるいは証券の均衡期待リターンを求めるというプロセスになります。通常の平均分散アプローチでは、ヒストリカルデータなどを使って期待リターンを求めます。しかし、この方法だと推定誤差が大きくなってしまうためブラックリッターマン砲では直接的に期待リターンは求めません。
そこでブラックリッターマン法では逆算的な考え方を用います。もし、市場が効率的であるならば現在の市場における時価総額ウェイトはマーケットポートフォリオであり、これがマーケットが想定している推定リスクとリターンを用いて最適化した結果得られたものと一致すると考えます。
つまり平均分散アプローチを実行した結果が、今の時価総額ウェイトのポートフォリオになっていると考えるのです。従って平均分散アプローチの逆手順を行うように、時価総額ウェイトから、逆算的に推定リターンを得ようというのがここでのアプローチになります。
この手法はReverse Optimization と呼ばれています。
具体的にどのようにすれば期待リターンを求められるのか考えていきます。
平均分散アプローチで用いられる効用関数を以下のように定義します。
ここで、$\delta$はリスク回避度を占めるパラメータ、$\Sigma$は分散共分散行列、$\Pi$は期待リターン、$w$は各資産のウェイトを示しています。
この効用関数を最大化するためには、$U$を$w$で微分した結果が0になる必要があります。
これを整理すると、
となり、期待リターンが求まることがわかります。
今、平均分散アプローチを実行した結果として、マーケットポートフォリオである時価総額加重のポートフォリオが存在していると仮定するので、$w$は時価総額ウェイトになります。
投資家の見通しを反映する
ブラックリッターマンモデルにおける続いてのステップは投資家の見通しを前のステップで求めた均衡期待リターンにブレンドするということです。例えば、日本株は米国株を2%アウトパフォームするだろう。A株のリターンは5%になるだろう。と言ったような見通しを推定に用いるリターンに反映することができます。
この時どのくらいの確信度で、これらの見通しが合っていると思うかは投資家によって異なり、状況によっても変わってきます。そこでブラックリッターマンモデルでは、どのくらいの確信度でこれらの見通しが当たっていると考えているかという部分も反映して推定に用いるリターンを更新します。
確信度が高い場合には、ステップ1で求めた均衡期待リターンよりも、投資家の見通しが重視されるのに対して、確信度が低い場合には、投資家の見通しはあまり反映されず均衡期待リターンがベースになるようにリターンが更新されます。
具体的に数式で見てみます。
投資家の見通しを$P$と$Q$、確信度を$\Omega$によって表します。
例えば、S&P,DAX,TOPIX,米国債券ETF、世界国債除く米国、REIT、金、原油、USD,EURの8資産のポートフォリオ構築を行っていると仮定します。
この時に、以下の2つの見通しを持っていたとします。
1. S&PがDAXとTOPIXを3%アウトパフォームするだろう。確信度は10%(正確には確信度は、この分布の分散)
2. 米国債券ETFは世界債券除く米国を2%アウトパフォームするだろう。確信度は5%
これを表現すると、
リターンとリスクの更新
上記の投資家の見通しをもとに、最初に推定した、均衡期待リターンを更新していきます。
リスクは以下のように更新できます。
これらが、投資家の見通しを反映した期待リターンと、リスクになります。
最適ウェイトの算出
前項で更新したリターンとリスクを使って、平均分散アプローチに基づいて求められる最適なウェイトは、最初に確認したように、効用関数を最大化するウェイトになるので、以下のようになります。
これは均衡期待リターンを求めたときと逆の手順を行っていることになります。
Pythonでの実装
簡単な例を使って、ブラックリッターマンモデルをPythonで実装してみます。
ライブラリのインポート
import pandas_datareader as web
from datetime import date
from dateutil.relativedelta import relativedelta
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
使用データの取得
#データ取得 S&P,DAX,TOPIX,米国債券ETF、世界国債除く米国、REIT、金、原油、USD,EUR
date_e = date.today() - relativedelta(days=1)
date_s = date_e - relativedelta(years=1)
price = web.stooq.StooqDailyReader(['^SPX','^DAX','^TPX','AGG.US','IGOV.US','REET.US', 'GOLD.US','WTI.US','USDJPY','EURJPY'], start=date_s, end=date_e,).read().sort_index()
このままだと価格なので、リターンに変換します。
#リターンデータに加工
rtn = price['Close'].pct_change().dropna()
display(rtn.head())
rtn.describe()
ブラックリッターマン法の実装
# ウェイト
n = len(rtn.columns)
w = np.array([[1./n]*n]).T #本来は時価総額加重だが、データがないため1/Nで代用
Sigma = rtn.cov()
# パラメータdelta
delta = 2.5
# パラメータtau
tau = 0.05
# 均衡リターン(reverse optimization)
pai = delta * np.dot(Sigma, w)
#投資家の見通し
P = np.array([
[1,-0.5,-0.5,0,0,0,0,0], #SP-0.2DAX-0.8TOPIX = 0.03
[0,0,0,1,-1,0,0,0]]) #AGG-IGOV=0.02
Q = np.array([[0.03],[0.02]])
Omega = np.array([
[0.1**2,0], #確信度10%
[0,0.05**2]]) #確信度5%
# 均衡リターンの更新
pai_bl = np.dot(np.linalg.inv(np.linalg.inv(np.dot(tau,Sigma)) + np.dot(np.dot(P.T, np.linalg.inv(Omega)), P)),np.dot(np.linalg.inv(np.dot(tau,Sigma)),pai) + np.dot(np.dot(P.T, np.linalg.inv(Omega)), Q))
#以下も同様の結果を得る
# pai_bl = pai + np.dot( np.dot( tau*np.dot(Sigma,P.T), np.linalg.inv(tau*np.dot(np.dot(P,Sigma),P.T)+Omega)), (Q-np.dot(P,pai)))
Sigma_bl = Sigma + np.linalg.inv(np.linalg.inv(np.dot(tau,Sigma)) + np.dot(np.dot(P.T, np.linalg.inv(Omega)), P))
#以下も同様の結果
# Sigma_bl = Sigma + tau*Sigma - tau*np.dot( np.dot( np.dot(Sigma,P.T), np.linalg.inv(tau*np.dot(np.dot(P,Sigma),P.T)+Omega)), tau*np.dot(P,Sigma))
# Forward Optimizationをして最適ウェイトを求める
w_bl = np.dot(np.linalg.inv(delta*Sigma_bl), pai_bl)
df = pd.DataFrame([w.reshape(n),w_bl.reshape(n)],
columns=rtn.columns,
index=['before','after'])
df.T.plot(kind='bar')
これを実行すると次のように、事前のウェイトと、事後のウェイトが表示されます。
事前ウェイトは平均分散アプローチでは時価総額ウェイトですが、今回は、データ取得の都合上、等ウェイトを使っています。
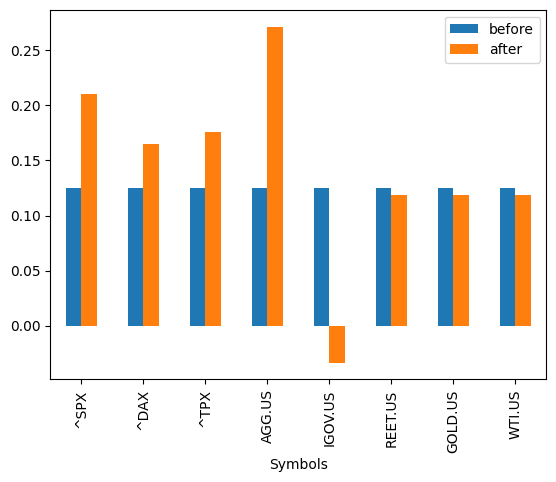
投資家の見通しは、説明と同様に、
1. S&PがDAXとTOPIXを3%アウトパフォームするだろう。確信度は10%(正確には確信度は、この分布の分散)
2. 米国債券ETFは世界債券除く米国を2%アウトパフォームするだろう。確信度は5%
という2つを反映しています。その結果、株のウェイトが全体的に上昇し、米債の方が、全世界債券よりウェイトが大きくなるように事後のウェイトは変化していることが確認できます。
パラメーター$\delta$や$\tau$の値を調整することによって、どのくらい大きく変化させるかを調整することができます。
このコード全体は以下のGoogle Colabで利用可能です。
コード全体はこちら



