【証券分析10-1】最小分散ポートフォリオとは

ポートフォリオ理論の基礎として、平均分散アプローチを紹介しましたが、これを活用するためには、期待リターンとリスク、各資産間の相関が必要になります。
しかし、これまでの記事でも確認したように期待リターンをどのように推定するかという問題は非常に難しい問題です。
それに比べて、リスクや相関は過去の時系列からの乖離が比較的少なく、推定しやすいです。
その性質を利用して、リスクのみに着目したアロケーション手法が提案されています。
その代表的な手法である、最小分散ポートフォリオとリスクパリティ―ポートフォリオについて、これからの数回で確認していきたいと思います。

最小分散ポートフォリオとは

以前の記事でも紹介したように、最小分散ポートフォリオとは、効率的フロンティアの中で、最もリスクの小さいポートフォリオのことを示しています。

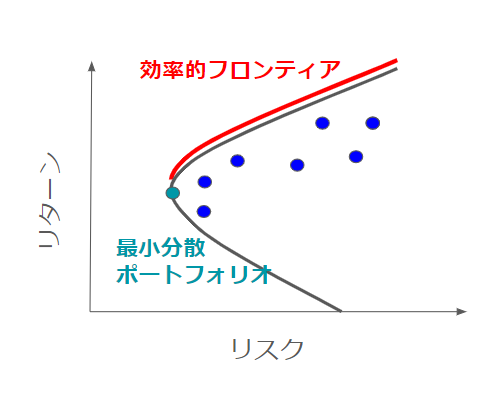
CAPMに基づくと、最小分散ポートフォリオは無リスク資産が存在する状況で、最適なポートフォリオではありませんが、実務においては、時価総額加重平均のポートフォリオよりも、パフォーマンスがいいといった研究結果もあります。
その他に最小分散ポートフォリオが好まれる理由としては、推定の難しい期待リターン情報が必要ないからということが挙げられます。一般的に、リターンの推定誤差よりも分散の推定リスクの方が小さいため、安定した結果が得られやすいのです。

最小分散ポートフォリオの導出

2資産の場合

ポートフォリオの分散は
$$\quad \sigma_P=\sqrt{w_{1}^2 \sigma_A^2+w_{2}^2 \sigma_B^2+2 w_{1} w_{2} \rho \sigma_A \sigma_B}$$

となります。
ウェイトの合計は1になるので、
$$w_{1} + w_{2} = 1$$

を使って、
$$\operatorname{minimize} \quad \sigma_P=\sqrt{w^2 \sigma_A^2+(1-w)^2 \sigma_B^2+2 w(1-w) \rho \sigma_A \sigma_B}$$

という最適化問題を解くことになります。
$w$で微分して0になるwが求めたいウェイトになるので、
$$\frac{d}{d w} \sigma_{p}^2=0$$

を解くことになります。
これに先ほどの標準偏差を求める式を代入すると、
$$\frac{d}{d w} \sigma_P^2=2 w \sigma_A^2-2 \sigma_B^2+2 w \sigma_B^2+2 \rho \sigma_A \sigma_B-4 w \rho \sigma_A \sigma_B$$

となるので、$=0$として$w$について解くと、

$$2 w \sigma_A^2-2 \sigma_B^2+2 w \sigma_B^2+2 \rho \sigma_A \sigma_B-4 w \rho \sigma_A \sigma_B=0$$

$$w=\frac{\sigma_B^2-\rho \sigma_A \sigma_B}{\sigma_A^2+\sigma_B^2-2 \rho \sigma_A \sigma_B}$$

となり解を得ます。

この$w$は$w_{1}$にあたるので、$w_{2}$は
$$w_{2}=1-w_{1}\\ =\frac{\sigma_A^2-\rho \sigma_A \sigma_B}{\sigma_A^2+\sigma_B^2-2 \rho \sigma_A \sigma_B}$$

となります。

多資産の場合

多資産の場合も2資産の場合と同様にポートフォリオの標準偏差を最小化するという最適化問題を解きます。
$$\operatorname{minimize} \sqrt{\mathbf{w^{T} \Sigma w}}$$

$$\text{subject to} \sum_{i=1}^{n} w_{i} = \mathbf{w e}= 1$$

という最適化問題を解くことになります。
この問題はPythonなどを使えば簡単に最適化問題として解を得ることができます。

最小分散ポートフォリオの実装

ここまでの議論をもとに実際にPythonで最小分散ポートフォリオのウェイトを求めてみます。
最適化にはPythonのscipyを使います。

import scipy.optimize as op
import pandas as pd
import numpy as np
def cal_min_vol(Sigma):
  #目的関数の設定
  def min_vol(w):
    var = np.dot(w.T, np.dot(Sigma, w)) 
    return var
  n = Sigma.shape[0]
  #制約条件
  cons = [{'type': 'eq', 'fun': lambda x: np.sum(x) - 1}]
  bnds = [(0, None)] * n 

  #初期値  
  x0 = [1./n] * n
  #最適化実行
  opts = op.minimize(fun=min_vol, x0=x0, method='SLSQP', bounds=bnds, constraints=cons)
  return opts['x']

この関数を、例えば、リスクが6%と13%相関が-0.2の2資産に適用した場合を見てみます。

s1 = 0.13
s2 = 0.06
rho = -0.2
Sigma = np.array([[s1*s1, rho*s1*s2],[rho*s1*s2, s2*s2]])
cal_min_vol(Sigma)

array([0.21845893, 0.78154107])

この結果を、解析的に解いて求めた2資産の場合のウェイト式に当てはめた場合と比較すると、

w1 = (s2**2-rho*s1*s2)/(s1**2 + s2**2 - 2*rho*s1*s2)
print(w1)
w2 = (s1**2-rho*s1*s2)/(s1**2 + s2**2 - 2*rho*s1*s2)
print(w2)

0.21845893310753595
0.7815410668924639

このように概ね結果が一致していることが確認できます。

多資産の場合でも、この関数を使って、各資産の最適ウェイトを求めることができます。

#4資産の場合
s1 = 0.13
s2 = 0.06
s3 = 0.03
s4 = 0.08
rho12 = 0.5
rho13 = 0.2
rho14 = -0.3
rho23 = 0.4
rho24 = -0.1
rho34 = 0.2
Sigma = np.array([
    [s1**2, rho12*s1*s2, rho13*s1*s3, rho14*s1*s4],
     [rho12*s1*s2, s2**2, rho23*s2*s3, rho24*s2*s4],
    [rho13*s1*s3, rho23*s2*s3, s3*s3, rho34*s3*s4],
    [rho14*s1*s4, rho24*s2*s4, rho34*s3*s4, s4*s4]
    ])
w = cal_min_vol(Sigma)
w

array([0.00936281, 0.06587514, 0.84607625, 0.0786858 ])