効率的フロンティアとは何か、以前の記事で紹介しましたが、今回は、実際にその効率的フロンティアを描いてみたいと思います。
Pythonを使って、効率的フロンティアを表示していきます。
データ取得
今回は、TOPIXコア30の日次データを使っていきたいと思います。
#TOPIX銘柄コードの取得
import requests
import pandas as pd
import pandas_datareader as web
from datetime import date
from dateutil.relativedelta import relativedelta
# CSVファイルのURL
url = "https://www.jpx.co.jp/markets/indices/topix/tvdivq00000030ne-att/topixweight_j.csv"
# HTTPリクエストを送信してファイルをダウンロード
response = requests.get(url)
# ステータスコードが200(成功)の場合
if response.status_code == 200:
# ダウンロードしたCSVデータをファイルに保存
with open("topixweight_j.csv", "wb") as f:
f.write(response.content)
# ファイルをPandas DataFrameに読み込む
data_df = pd.read_csv("/content/topixweight_j.csv",encoding='shift-jis')
else:
print(f"Failed to download the file. Status code: {response.status_code}")
#Core30の銘柄を取り出す
topix_core30 = list(data_df[data_df['ニューインデックス区分']=='TOPIX Core30']['コード'].astype(int).astype(str))
ticker_list = [i + '.JP' for i in topix_core30]
#データ取得
date_e = date.today() - relativedelta(days=1)
date_s = date_e - relativedelta(years=1)
price = web.stooq.StooqDailyReader(ticker_list, start=date_s, end=date_e,).read().sort_index()
rtn = price['Close'].pct_change().dropna()
PyPortfolioOptを使った効率的フロンティア
ポートフォリオ最適化ライブラリの一つであるPyPortfolioOptを使って、効率的フロンティアを表示していきます。
このライブラリは、価格もしくはリターンのデータ系列を入力にすることで、指定したリターンやリスクにおける最も効率的なウェイトを返してくれる関数があります。
まずは、installします。
! pip install PyPortfolioOpt
データから期待リターンと分散共分散行列を推定します。
from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
mu = expected_returns.mean_historical_return(rtn,returns_data=True) # リターンの計算
S = risk_models.sample_cov(rtn,returns_data=True) # リスク:標本共分散の計算
ef = EfficientFrontier(mu, S)
ターゲットとなるリターンを少しずつ変化させながらその時のリスクを取得することで、リターンリスク平面の効率的フロンティア上の点を取得していきます。
import matplotlib.pyplot as plt
import numpy as np
target_rtn_list = np.arange(round(np.amin(mu),3), round(np.amax(mu), 3), 0.001)
plot_rtn = []
plot_risk = []
for target_rtn in target_rtn_list:
w = ef.efficient_return(target_return=target_rtn) #ターゲットリターンに対応するウェイトを得る
w = ef.clean_weights() #ウェイトを丸める
pf = ef.portfolio_performance() #この時のリスクとリターンを得る
plot_rtn.append(pf[0])
plot_risk.append(pf[1])
最後にプロットします。
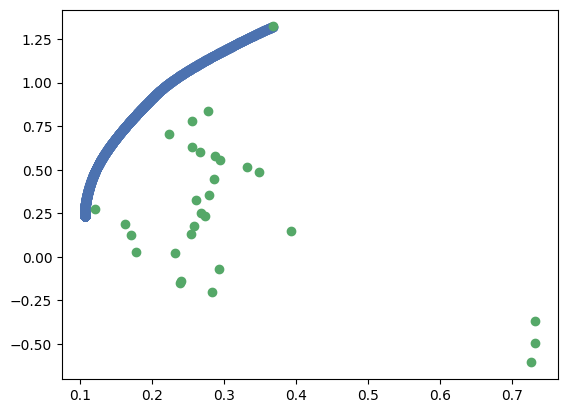
plt.scatter(plot_risk, plot_rtn) #効率的フロンティア
plt.scatter(np.sqrt(np.diag(S)),mu) #個別銘柄
このように効率的フロンティアを描くことができました。
個別銘柄は緑色のプロットです。
cvxpyを使った最適化による効率的フロンティア
次に、PyPortfolioOptを使わず、自分で最適化の数式を定義して、求める方法を紹介していきます。
最適化ライブラリであるcvxpyを使っていきます。
! pip install cvxpy
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt
returns = rtn.mean().values
covariance_matrix = rtn.cov().values
num_assets = len(rtn.columns)
# 最適化問題の変数
weights = cp.Variable(num_assets)
expected_return = returns @ weights
risk = cp.quad_form(weights, covariance_matrix)
# リスクの上限を設定
risk_constraint = cp.Parameter(nonneg=True)
constraints = [
cp.sum(weights) == 1, # ウェイトの合計が1
weights >= 0, # ウェイトは非負
expected_return >= 0, # 期待リターンは非負
risk <= risk_constraint
]
# 最適化問題の目的関数
objective = cp.Maximize(expected_return)
# 最適化問題を構築
problem = cp.Problem(objective, constraints)
# 効率的フロンティアを計算する範囲のリスク値を設定
risk_values = np.linspace(0, 0.05**2, 100)
# 効率的フロンティア上のポートフォリオの期待リターンを保存するリスト
expected_return_values = []
# リスク値を変えながら最適化問題を解く
for risk_val in risk_values:
risk_constraint.value = risk_val
problem.solve()
expected_return_values.append(expected_return.value)
# 結果をプロット
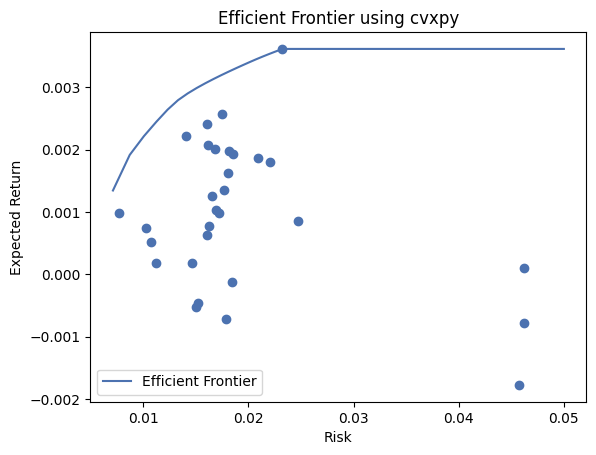
plt.plot(np.sqrt(risk_values), expected_return_values, label='Efficient Frontier')
plt.scatter(np.sqrt(np.diag(covariance_matrix)),returns) #個別銘柄
plt.xlabel('Risk')
plt.ylabel('Expected Return')
plt.title('Efficient Frontier using cvxpy')
plt.legend()
plt.show()
最適化においては、制約条件として、ウェイトの合計が1、ウェイトは非負、期待リターン非負、リスクを指定値という条件を設け、リスクを指定した時にリターンを最大にするウェイトを求めます。
これを実行すると以下のように効率的フロンティアを表示できます。
この時、途中で直線になっているのは、ウェイト非負でレバレッジを使えないためです。
今回のコード全体はこちら



