少し投資について勉強すると、ベータという言葉を目にすることがあるのではないでしょうか?
しかし、このベータが何を示すものなのか、しっかりと理解できている人は少ないのではないかと思います。
今回は、このベータと呼ばれるものの正体を見ていきます。
前提知識
ベータを理解するにあたって、ここまでの記事で紹介してきた、平均分散アプローチや効率的フロンティアがどんなものであるか理解しておく必要があります。まだ、これらがよくわかっていない場合は、過去の記事を確認してみてください。
また、今回紹介するベータを説明するには、CAPM第2定理という定理を紹介します。CAPM第2定理の説明では第1定理の内容も使用するので、CAPM第1定理についても前回の記事であるかっているので、ぜひ確認してみてください。
CAPM第2定理
それでは、本題のベータの正体に迫っていきます。ベータは、CAPM第2定理という定理の中で出てくる概念になりますので、このCAPM第2定理について、まずは見ていきます。
結論
CAPM第2定理の結論は、次のようになります。
証券i=1,2,…nが存在するとき、各証券のリターンを$r_{i}$として、これら証券市場の市場ポートフォリオのリターンは$r_{M}=\sum_{i=1}^{n}w_{i}r_{i}$とする。
この時、証券iの期待リターン$E[r_{i}]$は、リスクフリーレート(無リスク資産のリターン)を$r_{f}$として、
とできる。
この時、
である。
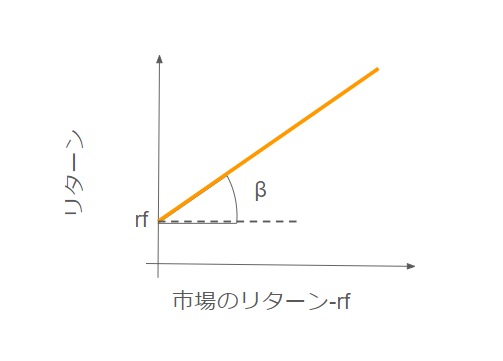
イメージは回帰
文章にすると複雑に見えますが、この定理は、
という回帰式をイメージすると理解しやすくなります。
これは
$E[r_{i}]$を$y$
$r_{f}$を$b$
$\beta_{i}$を$a$
$(E[r_{m}]-r_{f})$を$x$
と置き換えると見慣れた回帰式に見えてきます。
ここで
となる理由は、端回帰分析の最小二乗法における係数の推定式と比較すると理解しやすいです。
端回帰の最小二乗法における係数推定の詳細は以下のサイトなどを参考にしてください。
参考サイト
単回帰の係数は
のように最小二乗法を使うと求めることができます。
これを先ほどのベータの式と比較すると、
は
の部分に対応します。
したがって$\beta$は次のようにも書けます。
株式のベータを実際に求めてみよう
それでは、実際にトヨタのリターンデータとTOPIXのリターンデータを使って、トヨタのベータを求めてみましょう。
import pandas_datareader as web
from datetime import date
from dateutil.relativedelta import relativedelta
date_e = date.today() - relativedelta(days=1)
date_s = date_e - relativedelta(years=1)
toyota = web.stooq.StooqDailyReader('7203.JP', start=date_s, end=date_e,).read().sort_index()
topix = web.stooq.StooqDailyReader('^TPX', start=date_s, end=date_e).read().sort_index()
まずはデータを取得します。今回は、Stooqというサイトから過去1年の株価データを取得します。
ax = toyota['Close'].plot(label='TOYOTA',legend=True)
ax = topix['Close'].plot(ax=ax, legend=True, label='TOPIX')
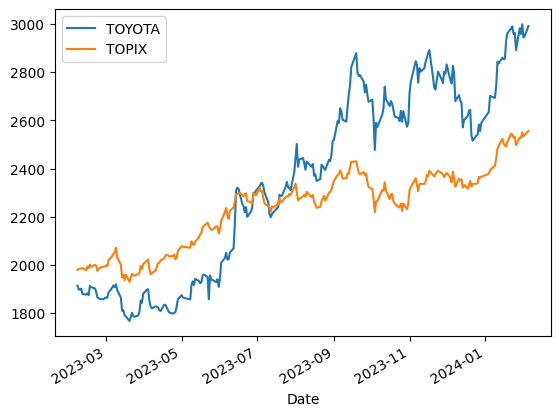
プロットするとこのようになっています。
早速、sklearnを使って、単回帰分析を行い、係数を推定します。
from sklearn.linear_model import LinearRegression
#ベータの算出
rf = 0 #リスクフリーレートは0とする
X = topix[['Close']].pct_change().dropna() - rf #.pct_change()によってリターンに変換
y = toyota[['Close']].pct_change().dropna() - rf
model_lr = LinearRegression()
model_lr.fit(X, y)
print('y= %.3fx + %.3f' % (model_lr.coef_ , model_lr.intercept_))
y= 1.379x + 0.000
このように表示される1.379がトヨタのこの期間のベータになります。
ここからわかるように、ベータの値は、入力に依存するので、計算期間によって、変化します。
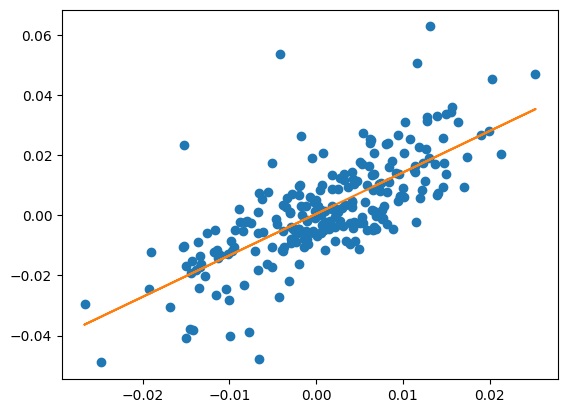
プロットで確認すると以下のようになります。
import matplotlib.pyplot as plt
plt.plot(X, y, 'o')
plt.plot(X, model_lr.predict(X), linestyle="solid")
plt.show()
print('β: %.3f' %model_lr.coef_)
print('y= %.3fx + %.3f' % (model_lr.coef_ , model_lr.intercept_))
print('決定係数 R^2: ', model_lr.score(X, y))