株式をはじめとする多くの投資には、運の要素が非常に大きく影響してくるということは、多くの人が感じていることではないでしょうか。
では一体、投資のパフォーマンスにおいて、実力の運の影響はどういった関係になっているのでしょうか。
今回は、モンテカルロシミュレーションを用いて、この疑問について考えてみたいと思います。
単純化した世界で収益を考える
まずは、今回のシミュレーションの設定を考えてみます。
簡単にするために、ここでは以下のようなゲームを考えます。
1. 投資家は毎日1回、明日の株価が上がるか下がるか予測する。
2. 予測が当たっていた場合には+1の収益を得る。一方で、外れた場合には、-1の収益を得る。
3. 必ず毎日判断を行いn日このゲームに参加する。
4. 投資家の株価予測の精度は、その投資家の実力を示しており、〇%の確率で方向性を正しく予測できる。
モンテカルロシミュレーションの実装
この前提に基づいてモンテカルロシミュレーションのプログラムを書いてみます。
まずは、51%の確率で方向性を予測できる投資家が、100日取引する場合をシミュレーションしてみます。
モンテカルロシミュレーションの実行回数は10000回です。
-
シミュレーションの設定:
– 1日の取引における勝率(株価が上がる確率)を51%とします。
– 各1日の収益は、予測が当たった場合に+1、外れた場合に-1とします。
– 取引日数 を決めます(例えば、100日)。
– シミュレーションの回数 を決めます(例えば、10000回)。 -
シミュレーションの実行:
– ランダムに株価が上がるか下がるかを予測し、その収益を計算します。
– これを 日間繰り返し、総収益を記録します。
– このシミュレーションを 回繰り返し、収益の分布を求めます。 -
収益分布の可視化:
– シミュレーション結果をヒストグラムとしてプロットし、収益の分布を可視化します。
それでは、Pythonで実装してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_days = 100 # 取引日数
m_simulations = 10000 # シミュレーションの回数
win_prob = 0.51 # 株価が上がる確率
# シミュレーションの実行
results = []
for _ in range(m_simulations):
# 各日の収益をランダムに決定
daily_outcomes = np.random.choice([1, -1], size=n_days, p=[win_prob, 1 - win_prob])
total_profit = np.sum(daily_outcomes)
results.append(total_profit)
# 結果を可視化
plt.hist(results, bins=30, edgecolor='black', alpha=0.7)
plt.title(f'Profit Distribution over {n_days} Days ({m_simulations} Simulations)')
plt.xlabel('Total Profit')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()
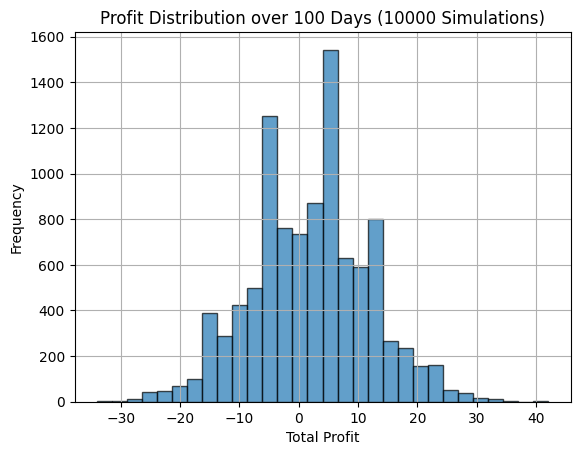
やや右側に分布が寄っているようには見えますが、結構マイナス側にも分布していますね。
では、このとき、収益が0より大きいのは全体のうちのどのくらいになるのでしょうか?
# 収益が0より大きい回数をカウント
positive_results = sum(1 for result in results if result > 0)
# 確率を計算
probability_positive_profit = positive_results / m_simulations
probability_positive_profit
今回の場合は、0.5374となりました。
つまり、今回のシミュレーションの設定では54%くらいの確率で、最終的な収益は0より大きくなったということです。毎回の投資判断で51%の精度で当てらて100回くらい取引すれば、54%くらいでは利益が出そうということです。
これを低いと考えるか高いと考えるかは人それぞれだと思います。ここで注目したいのは、一般的な人より正しく予測(51%の確率)できているにも関わらず、大きくマイナスになっている場合も存在するということです。これを見ることで、いかに運の要素が大きいかを感じることができるのではないでしょうか。
予測精度と取引回数を変えてみる
では、いったいどのくらいの実力(予測精度)があれば、かなりの確率で収益を出せるのでしょうか?
そのためには、実力だけではなく、投資回数も増やす必要があります。対数の法則によって、投資回数が増えれば、その分だけ、実際の実力に近い結果が得られるようになります。
そこで、先ほどのコードをベースに、予測確率と、取引日数をいくつかのパターンで試してみます。
from scipy import stats
import pandas as pd
import numpy as np
def monte_carlo_simulation(n_days, win_prob, m_simulations=10000):
results = []
for _ in range(m_simulations):
daily_outcomes = np.random.choice([1, -1], size=n_days, p=[win_prob, 1 - win_prob])
total_profit = np.sum(daily_outcomes)
results.append(total_profit)
avg_profit = np.mean(results)
std_profit = np.std(results)
# t検定を実行
t_stat, p_value = stats.ttest_1samp(results, 0)
# 収益が0より大きい回数をカウント
positive_results = sum(1 for result in results if result > 0)
# 確率を計算
probability_positive_profit = positive_results / m_simulations
return avg_profit, std_profit, t_stat, p_value, probability_positive_profit
# パラメータの設定
n_days_list = [10, 50, 100, 250, 520, 2500, 10000]
win_prob_list = [0.49, 0.5,0.501,0.505, 0.51, 0.55,0.6]
# 結果を格納するリスト
data = []
# シミュレーションを実行
for n_days in n_days_list:
for win_prob in win_prob_list:
avg_profit, std_profit, t_stat, p_value,probability_positive_profit = monte_carlo_simulation(n_days, win_prob)
data.append({
'n_days': n_days,
'win_prob': win_prob,
'avg_profit': avg_profit,
'std_profit': std_profit,
't_stat': t_stat,
'p_value': p_value,
'positive_profit': probability_positive_profit
})
# データフレームにまとめる
df = pd.DataFrame(data)
結果
投資日数を示すn_daysは以下のパターンを試します。
n_days_list = [10, 50, 100, 250, 520, 2500, 10000]
実力を示す、予測確率win_probは以下です。
win_prob_list = [0.49, 0.5,0.501,0.505, 0.51, 0.55,0.6]
ますは、投資日数が10日の場合
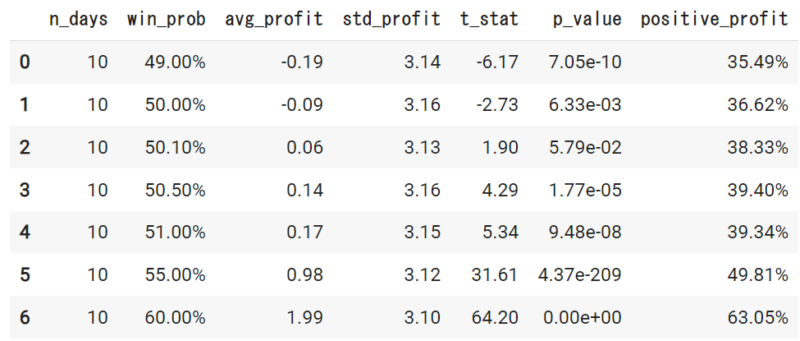
予測確率が60%でも最終収益がプラスになる確率positive_profitは63%ほどでした。
p値は0と異なる確率を示しています。
続いて、50日の場合
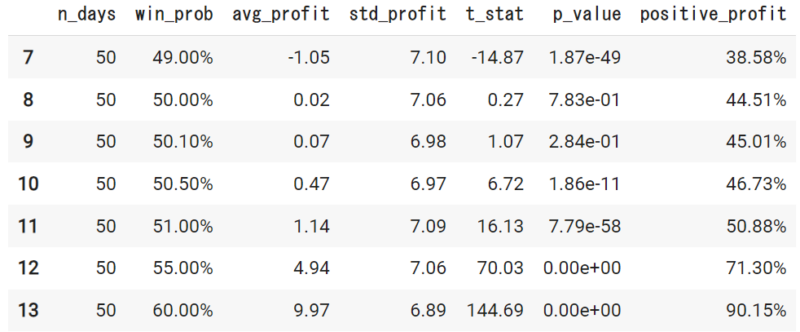
この場合は、60%くらいの精度で予測できていれば9割くらいはプラス収益になっています。55%の予測でも7割程度です。
予測精度が高ければ、それなりによさそうですね。
100日
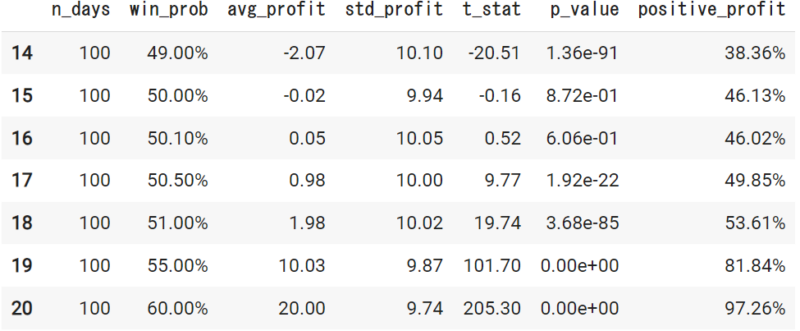
250日
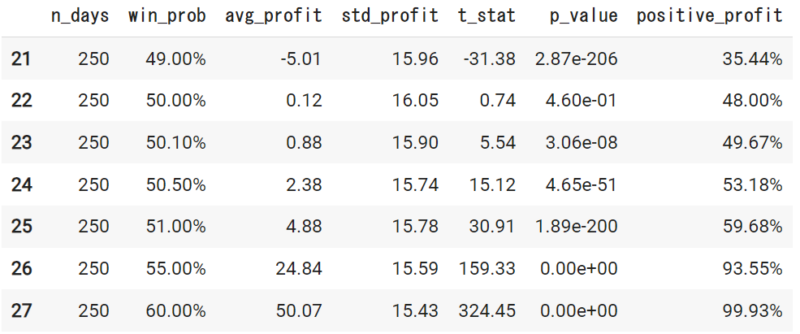
520日
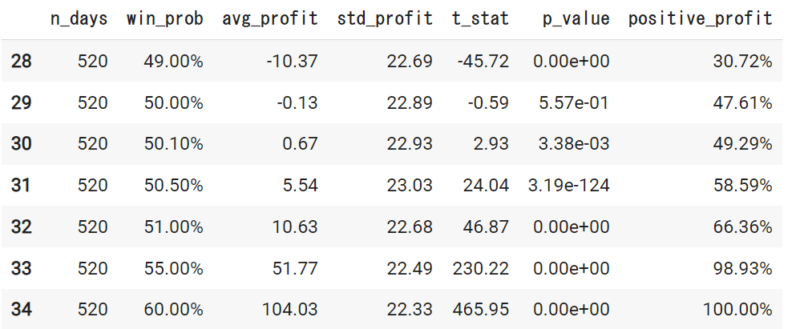
2500日
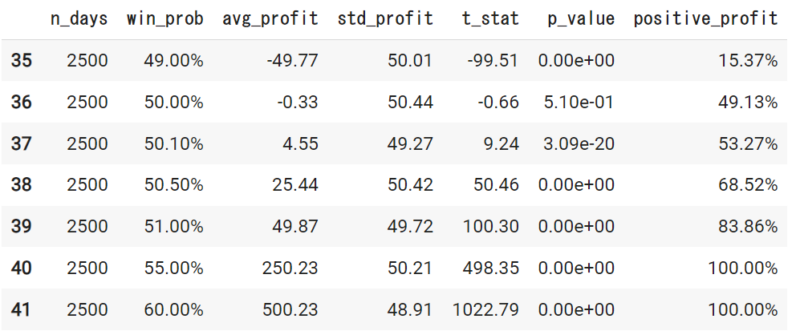
10000日
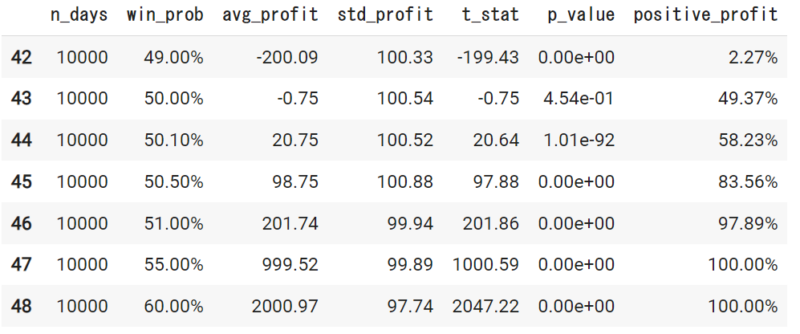
さて、取引日数を増やすにつれて50%からわずかに予測できているだけでも、収益の得られる可能性は高くなっているのが確認できます。
10000回取引するのであれば、51%くらいの予測精度が出ていれば、かなりの確率で収益はプラスになりそうです。
今回は単純化して、当たった場合も外れた場合も同じ大きさの利益または損失が発生する設定となっています。
しかし、実際の取引では、取引ごとに利益と損失の大きさは異なるケースがほとんどだと思いますので、より複雑になります。
例えば、よくトレンドフォローは小さくたくさん負けて、たまに大きく勝つといわれます。このように戦略の特性によっても変わってきますが、何はともあれ、統計的に収益がプラスになる方法を見つけて、それをたくさん取引することで、やっと想定される結果に近づくということではないでしょうか。
たとえ、毎日取引していて、51%の予測の実力を持っていたとしても、1年くらい(250日)の取引ではせいぜい6割くらいの確率でしか収益はプラスになりません。実力があっても運によって、4割くらいは負けます。
多少の運用期間の成績を見たところで、本当にそのファンドの運用者に実力があるのか、それともたまたま運がよかっただけなのかを見分けるのは非常に難しいことがこのシミュレーションを通じて少しでも感じていただけるといいかと思います。
ここで、もう一つ大切なのは、それなりに高い確率で予測できたとしても、取引できる回数が少ないと運によって、思ったような結果が得られない可能性が高くなるということです。
予測精度だけでなく、実際にその取引をどのくらい行えるかも考える必要があるということです。
最後に今回のコードはこちらのGoogleColabで実行できます。



